The goal of aerodynamics is to predict the flow around bodies and the forces the bodies experience. The only way for nature to communicate an aerodynamic force is through the pressure distribution over the body, and the shear stress distribution over the body.
Predicting this is done by mixing theory, empirical data, and computer simulations (CFD).
Table of Contents
Flow Types ↑
For most cases, continuum flow is investigated, in which the scalars pressure $p$, density $\rho$, temperature $T$, and vector velocity $\mathbf{V}$ are defined infinitesimally for each point in space. It's a good approximation, as long as the mean distance between molecules is small enough .
Inviscid flow is an approximation that assumes no "transport" phenomena - no flow friction, no mass diffusion, and no thermal conduction. In reality, these effects exist for for all flow, but for low viscosity fluids, like air, the effect is negligible, except for a thin region around a body - the boundary layer.
Flow can also be approximated as incompressible ($\rho = const$). Compressibility effects are less than 5% for Mach numbers of $M < 0.3$.
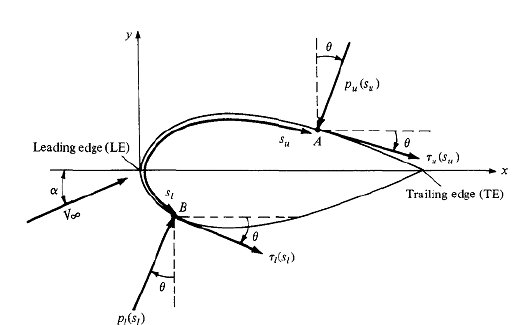
The local Mach number describes whether the flow in that region is subsonic $M < 1$, sonic $M=1$ or supersonic $M > 1$. Flows with a mix of subsonic and supersonic flow are called transonic. In subsonic flow, a disturbance propagates and can be felt in the entire flow field . In regions of supersonic flow, the disturbance can only go downstream.
Boundary Layer ↑
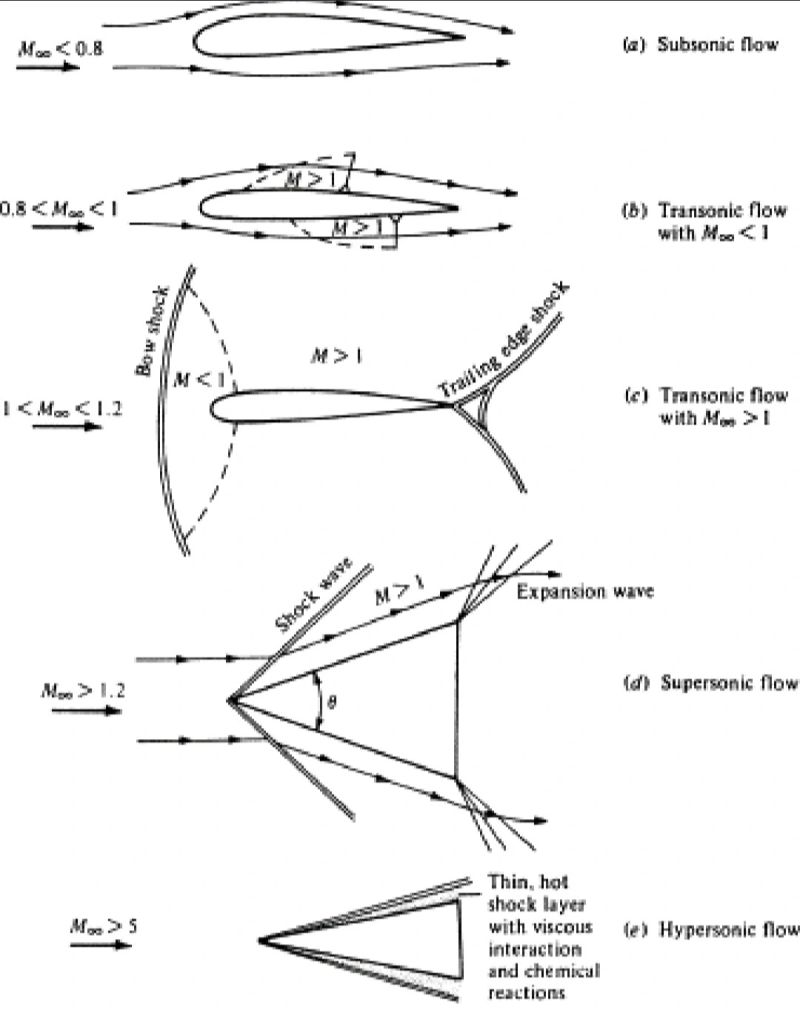
Friction in flow is the internal shear stress that causes a velocity gradient.
The boundary layer is where the velocity rapidly reduces from the free stream value $V_\infty$ to 0, due to the no-slip condition .
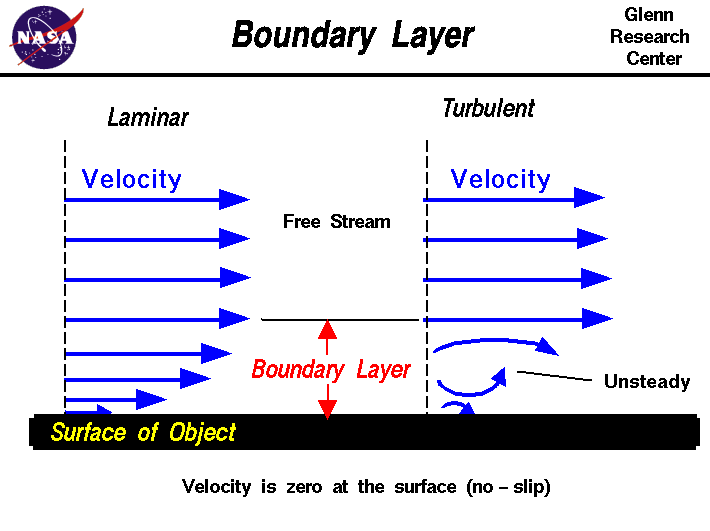
Prandtl's boundary layer theory revolutionized aerodynamics. He separated the flow into two parts - the approximately inviscid flow far away from the body , and the thin, viscous boundary layer .
There's a peculiar effect that allows ignoring the boundary layer in certain cases. If the flow is attached , imagine virtually extending the body, encompasing it's boundary layer, and solving for the inviscid flow. Then the pressure at the edge of the boundary layer (point $b$) is precisely equal (in theory and in practice) to the pressure at the real boundary of the body (point $a$):
Force Coefficients ↑
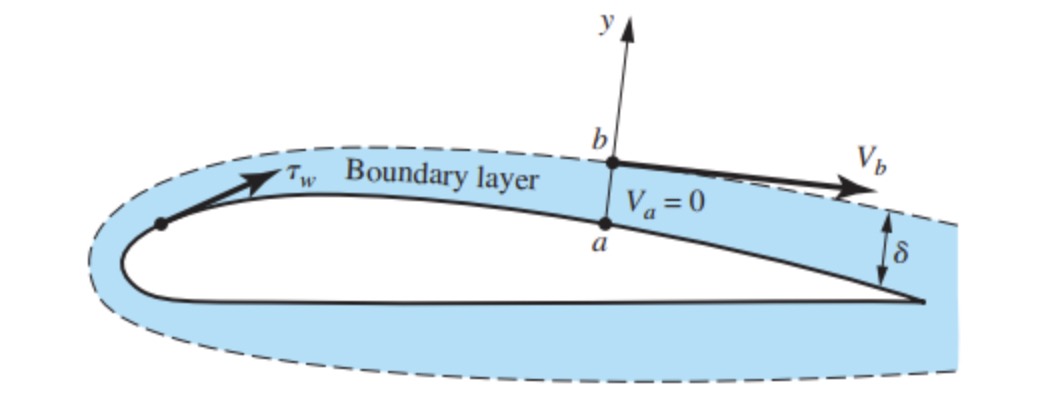
By definition, lift $\mathbf{L}$ is the force that the body experiences perpendicular to $V_\infty$, and drag $\mathbf{D}$, parallel to $V_\infty$. The resulting force $\mathbf{R}$ = $\mathbf{L}$ + $\mathbf{D}$ can also be split into normal $\mathbf{N}$ and axial $\mathbf{A}$ components, normal to the chord $c$, and parallel to it respectively.
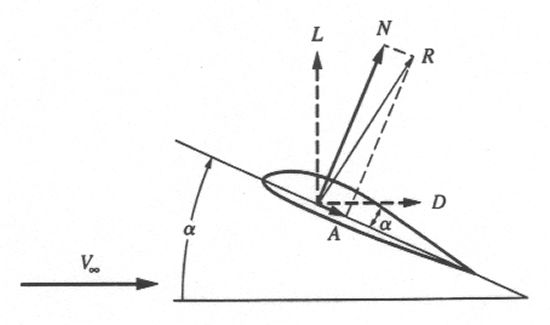
$$ \begin{aligned} L = N \cos \alpha - A \sin \alpha \\ D = N \sin \alpha + A \cos \alpha \end{aligned}$$
It's useful to define dimensionless coefficients, independent of the size of the body, and the dynamic pressure of the flow $q_\infty = 1/2 \rho V_\infty^2$, for example
$$ C_L = \frac{L}{q_\infty S} \quad ..., $$
where $S$ is any common reference area, depending on the use case .
Lowercase letters are used in 2D cases when the force is viewed per unit span (1 m): $c_l = L'/q_\infty S, \quad ...$
To practice, use Anderson's book, find how to calculate $c_l$ and $c_d$, using 2D pressure and shear stress distributions, and solve Example 1.1.The coefficients are dependent on other flow properties as well, notably the Reynolds number $Re$ and $M$. $Re$ is a scale parameter related to the ratio of inertial to viscous forces of the flow, and roughly predicts when the transition between laminar and turbulent flow occurs. $M$ is related to the compressibility effects that notacibly occur at $M > 0.3$.
Question: How do laminar and turbulent flow differ? Is laminar flow always better? Why do airplane wings have vortex generators, that intentionally create turbulent flow over part of the wing?When heat transfer is involved, other dimensionless parameters affect the coefficients, such as the ratio of specific heats $\gamma$, ratio of wall to freestream temperature $T_w/T_\infty$, and the Prandtl number $Pr = \mu_\infty c_p / k_\infty$, where $k_\infty$ is the thermal conductivitiy of the freestream.
In short, besides the body geometry, all of the above similarity parameters have to be equal in order to make comparison of aerodynamic characteristics meaningful.
Question: Which of the similarity parameters are important when building a wind tunnel scale model of a passenger aircraft? Can they be practically achieved at the same time?Juicy Vector Calculus ↑
The del operator $\nabla \circ$ is simply syntactic sugar for
$$\frac{\partial \circ}{\partial_x} + \frac{\partial \circ}{\partial_y} + \frac{\partial \circ}{\partial_z}, $$
where Cartesian 3D coordinates are assumed, but in principle it can be defined as the sum of partial derivatives in each direction in any coordinate system .
The circles denote that these are operators, therefore, they haven't acted on anything yet. Something should be there to fill them in. Whatever is put to the right of them is what they're eventually going to "eat". For example, for a vector field $\mathbf{A}$ this is the difference between
$$\nabla \circ \cdot \mathbf{A} \quad \text{and} \quad \mathbf{A} \cdot \nabla \circ $$
In the first case, the dot product expands to
$$ \frac{\partial A_x}{\partial_x} + \frac{\partial A_y}{\partial_y} + \frac{\partial A_z}{\partial_z} $$
and del has taken up the components of $\mathbf{A}$ to act on, therefore the result of this operation is a scalar. The second dot product expands to
$$A_x \frac{\partial \circ}{\partial_x} + A_y \frac{\partial \circ}{\partial_y} + A_z \frac{\partial \circ}{\partial_z}, $$
which is a sum of operators, like the original del, still waiting for something to eat.
Later on the substantial derivative is used, which uses the same principle:
$$ \frac{D \circ}{Dt} = \frac{\partial \circ}{\partial t} + \mathbf{V} \cdot \nabla \circ$$
Divergence of Velocity ↑
... is the time rate of change of the volume of a moving fluid element, per unit volume. This is a mouthful, but if you look at the voodoo derivation in Anderson's book, the result is that
$$ \nabla \cdot \mathbf{V} = \frac{1}{\delta \mathcal{V}} \frac{D (\delta \mathcal{V})}{Dt}, $$
which says intuitively that the divergence of the velocity field , measures how much a starting volume of particles grows/shrinks in size in time, per unit volume.
Question: The unit of $\nabla \cdot \mathbf{V}$ are $1/s$, check if the derivatives make sense with the units.Take $\nabla \cdot \mathbf{V} = -0.7327 /s$ at a point in a flow. A volume passing through that point would shrink 73 percent in 1 second. At that point compression occurs and density increases.
Question: Do the full Example 2.1 in Anderson's book for a more in-depth look.Mass can be neither created nor destroyed. ↑
For a given area the mass flow can be defined as:
$$\dot{m} = \rho V A.$$
Also, it's always nice to remember that $\rho V$ denotes mass flux in the direction of $V$:
$$\text{Mass flux} = \dot{m} / A = \rho V.$$
If a control volume is taken, conservation of mass means that the mass decrease inside the volume is equal to the mass leaving the volume through it's surface:
$$ - \frac{\partial}{\partial t} \iiint_\mathcal{V} \rho d\mathcal{V} = \iint_S \rho \mathbf{V} \cdot d\mathbf{S}$$
Question: What does the sign of the dot product $\rho \mathbf{V} \cdot d\mathbf{S}$ tell about outflow/inflow at that local surface?This is called the continuity equation, and expressed in integral form it's very powerful. It's not concerned with exactly what's happening in the flow, but over a finite space. If a certain point of the flow is of interest, then the differential formulation is more useful:
$$\frac{ \partial \rho }{\partial t} + \nabla \cdot (\rho \mathbf{V}) = 0$$
Remember how in electrodynamics the integral formulation of Maxwell's equation is more useful (when looking at circuits as a whole) and when the differential formulation is (when deriving electromagnetic waves at points in space).
